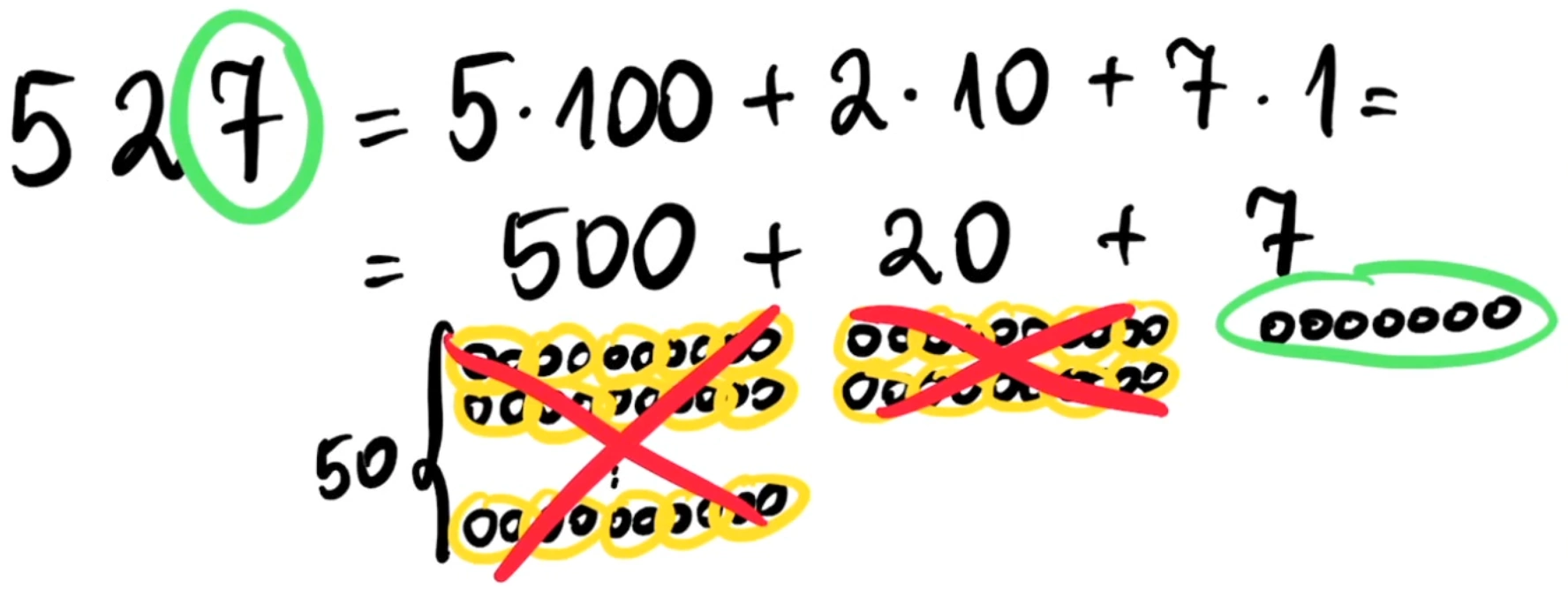
Cechy podzielności przez dowolną liczbę
Materiał wideo o cechach podzielności z wyjaśnieniem dlaczego to działa.
Narzekałem jakiś czas temu na brak dowodów przy prezentacji twierdzeń w szkołach podstawowych na przykładzie twierdzenia Pitagorasa. Zanim jednak w szkole pojawia się to twierdzenie, najpierw uczniowie rozstrzygają podzielność liczb. Dowiadują się na przykład, że liczba jest podzielna przez $3$, gdy jej suma cyfr jest podzielna przez $3$. Najczęściej niestety nie dowiadują się dlaczego ta reguła podzielności działa. Dzisiejszy materiał wideo, w którym to wyjaśniam, powinien odczarować ten temat i pokazać, że da się to jasno przekazać nie tylko w grupie zainteresowanych i wybitnych uczniów, ale w całej klasie.
Film
Uwagi dodatkowe
Z uwagi na obietnicę, że wyjaśnienie zajmie mniej niż kwadrans, nie pokazałem wprost cechy podzielności przez $4$ lub $8$. Wynikają one jednak bezpośrednio z zaprezentowanej metody.
Po cichu też pominąłem fakt sprawdzania podzielności przez liczby złożone (np. $6$). W takim przypadku zamiast zaprezentowanej metody optymalnie jest sprawdzać podzielność przez występujące w dzielniku potęgi liczb pierwszych z osobna. Przykładowo, żeby sprawdzić podzielność przez $12$, można sprawdzić podzielność przez $3$ i $4$. Być może jest to dobry temat na inny materiał.