Coś pozytywnego: Mistrzostwa Polski w Grach Matematycznych i Logicznych
Całkiem sensowna aktywność matematyczna dla najmłodszych
Wróciłem właśnie z synem z finału Mistrzostw Polski w Grach Matematycznych i Logicznych. Mój syn co prawda nie wygrał zawodów (nie liczyliśmy na to), ale wróciliśmy do domu w dobrych humorach. W mojej opinii zadania były całkiem sensowne, zupełnie inne nie tylko od zadań szkolnych, ale również od zadań jakie można spotkać na innych konkursach matematycznych. W tym wpisie przeanalizuję czym te zadania się różniły i przedstawię dlaczego uważam, że takie powinny być.
Zadania finałowe można znaleźć na stronie Mistrzostw. Organizatorem zawodów w Polsce jest Politechnika Wrocławska. Jakkolwiek uważam, że niecały kilometr dalej, po drugiej stronie ulicy, znajduje się znacznie ciekawsze miejsce do studiowania matematyki i informatyki, organizatorom nie można odmówić, że zawody się udały.
Zadania
Skupię się na kategorii CE, przeznaczonej dla uczniów klas 1-3 szkół podstawowych. Uczniowie startowali w dwóch sesjach jednogodzinnych, odbywających się w dwóch kolejnych dniach. Na każdej sesji mieli do rozwiązania pięć zadań.
Uczniowie, którzy rozumują jedynie w “szkolny” sposób (zgadnij na podstawie słów/fraz kluczowych “o $n$ więcej”, “jaka różnica”, “$n$ razy więcej” lub “dzielą się po równo”, czy liczby z opisu zadania trzeba do siebie dodać, odjąć, pomnożyć czy podzielić (a na tym polegają najtrudniejsze, tak zwane zadania z treścią, na egzaminach trzecioklasisty)), zakończyliby zawody z zerem punktów. W zbiorze dziesięciu zadań konkursowych dla tej kategorii wiekowej nie było ani jednego, które polegałoby jedynie na zrozumieniu treści, wydobyciu odpowiednich liczb z opisu oraz wykonania jednego działania.
Aby dobrze zrobić zadania i odnieść sukces należy:
- dobrze je zrozumieć i wziąć pod uwagę wszystkie warunki zadania,
- spróbować wiele możliwości w uporządkowany sposób, aby nie pominąć żadnej istotnej,
- mieć intuicję i spryt, co pozwala ominąć dużą liczbę sposobów, które nie prowadzą do rozwiązania,
- nie popełnić głupiego błędu.
Zadanie 1 z dnia pierwszego
Pierwsze zadanie pierwszego dnia polegało na podzieleniu figury geometrycznej na sześć identycznych części (z dokładnością do odwrócenia lub obrócenia).
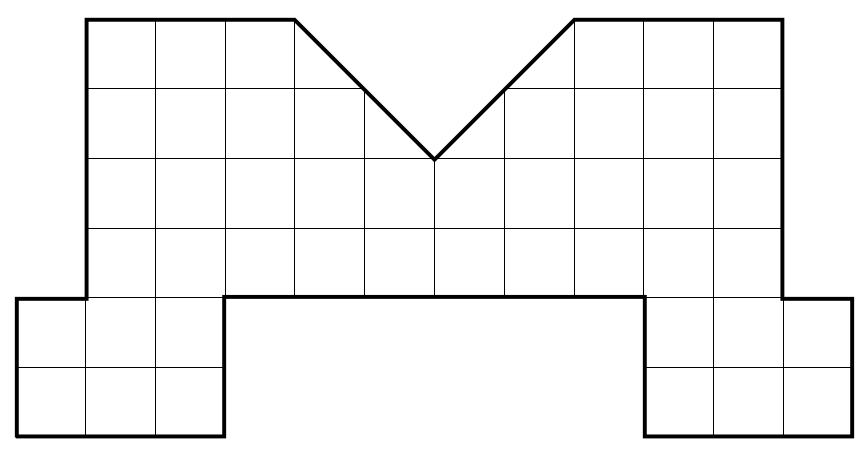
Figura z zadania 1 z dnia pierwszego GMiL.
Dobra intuicja polega tutaj na zauważeniu, że figura jest symetryczna osiowo, a więc być może dobrym pomysłem jest wykonać pierwsze cięcie wzdłuż osi symetrii (pionowej, w “ząbku” litery M), a następne cięcia może uda się zrobić symetrycznie po obu stronach. Dziecko nie musi w głowie używać pojęć symetria osiowa. Ma w ręku konkretny obiekt, a jeśli jest sprytne, mogłoby nawet wyjąć pomocniczą kartkę w kratkę i użyć nożyczek, żeby wyciąć szablon i sprawdzać czy części rzeczywiście się na siebie nakładają.
Zadanie 3 z dnia pierwszego
Innym dobrym przykładem jest zadanie trzecie z pierwszego dnia zawodów o wypełnianiu prostokąta klockami a’la tetris:
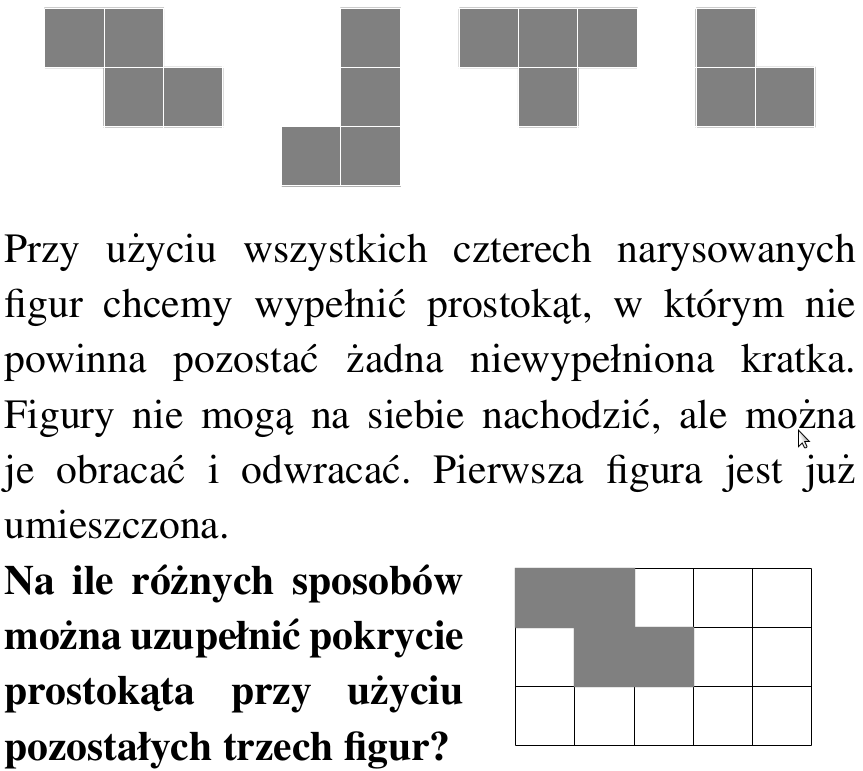
Treść zadania 3 z dnia pierwszego GMiL.
Tutaj dla odmiany kluczowe jest być uporządkowanym, aby nie pominąć żadnego sposobu. Moim zdaniem optymalnie byłoby zacząć od klocka w kształcie małego lub dużego L, aby zapełnić lewy dolny róg planszy, następnie skupić się na klocku w kształcie T, który będzie miał mało możliwych ustawień (szczególnie takich, w których można jeszcze dostawić kolejne duże lub małe L).
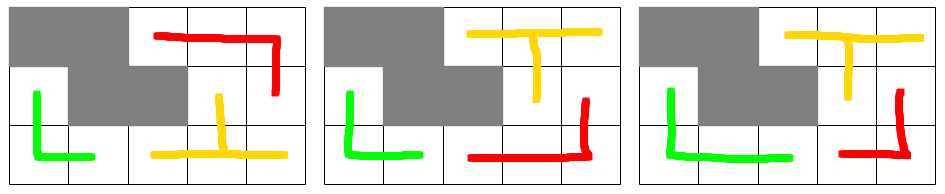
Rozwiązanie zadania 3 z dnia pierwszego GMiL. Wszystkie sposoby chyba najłatwiej znaleźć w kolejności: zielony, pomarańczowy i czerwony klocek.
Uważam umiejętność dostrzeżenia i systematycznego rozpatrzenia wszystkich możliwości za cenną (nie tylko w samej matematyce). W szkole zazwyczaj rozwiązywanie zadań metodą prób i błędów się tępi. Jasnym jest dla mnie, że gdy dzieci dorosną i będą w stadium formalnym, wtedy można i powinno się wymagać więcej, ale w pierwszych klasach szkoły podstawowej powinno się promować matematykę w formie ciekawych pomysłów, które można “dotknąć”. Szkoda, że albo się taką matematykę pomija, albo wręcz karci uczniów, którzy takiej matematyki próbują używać.
Przykładowe nietypowe rozumowanie
Weźmy przykładowe zadanie, które zaproponowałem w pierwszym bukiecie matematycznym. Suma dwóch liczb wynosi $20$, a ich różnica wynosi $4$. Ile równe są te liczby?
Szkoła, mniej więcej od klasy szóstej będzie wymagała od ucznia następującego rozumowania. Niech mniejsza liczba to $x$. Wtedy większa liczba to $x + 4$. Suma tych liczb to $2x + 4 = 20$. Rozwiązując równanie otrzymujemy $x = 8$, a więc te liczby to $8$ oraz $12$. Później, gdy uczniowie poznają układy równań, preferowane będzie rozwiązanie, w którym uczeń zapisze $x + y = 20$, $x - y = 4$ i rozwiąże ów układ metodą podstawiania lub metodą przeciwnych współczynników.
Przed klasą szóstą takich zadań się raczej unika. Tymczasem już ambitny pierwszoklasista mógłby metodą prób i błędów wyznaczyć rozwiązanie. Wcale nie trzeba próbować dziesiątek możliwości. Wystarczyłoby mieć wyczucie, że jedna z liczb musi być większa, a druga mniejsza niż $10$. Albo chociaż mieć wyczucie, że zwiększając jedną z liczb o $1$, drugą też trzeba zwiększyć o $1$, a więc suma zwiększa się o $2$, spróbować jakąś parę i zobaczyć czy wyszło za mało czy za dużo i ewentualnie poprawić swój “strzał” aż wyjdzie suma $20$. Tak jak wspomniałem, nauczyciel w edukacji początkowej nie pokaże uczniowi takiego zadania. A nauczyciel w klasach 4-8 nie doceni tego rozwiązania, skupiając się na tym, że uczeń “zgadywał”, albo jeżeli jest nieco bardziej merytoryczny to (częściowo) słusznie zwróci uwagę na to, że z takiego rozwiązania wynika jedynie, że $(8, 12)$ jest parą liczb, która spełnia warunki zadania, ale nie wynika, że nie ma innych par. W praktyce, z tego co napisałem nawet i to wynika, ale uczeń, który za pierwszym razem zaproponuje takie rozwiązanie, najprawdopodobniej nie będzie wiedział, że nauczycielowi trzeba dokładnie tłumaczyć, w jaki sposób myślał i na kartce zapisze jedynie samo rozwiązanie. Po tym jak zostanie negatywnie oceniony, następnym razem już nie spróbuje już tego typu rozumowania.
Moim zdaniem to szkoda, bo uczeń, który czuje liczby, jest na najlepszej drodze do zrozumienia wyrażeń algebraicznych w niedalekiej przyszłości. A może je rozumie, ale wygodniej było mu akurat skorzystać ze swojej liczbowej intuicji. Czy nie lepiej byłoby wytłumaczyć takiemu sprytnemu uczniowi dlaczego uwaga o tym, że im większa jedna z liczb, tym większa druga liczba, a więc i suma jest ważna i dlaczego z niej wynika, że rozwiązanie jeżeli istnieje to jest jedyne? Bo boimy się, że w innych warunkach egzaminatorzy nie zrozumieją takiego rozumowania i uczeń nie wstrzeli się w klucz? Nawet jeżeli, to nie wina ucznia, tylko egzaminatora i klucza oceniania.
Zadanie 1 z dnia drugiego
Omówmy jeszcze jedno zadanie konkursowe, tym razem z dnia drugiego GMiL. W zadaniu tym pięć osób chce usiąść w jednym rzędzie. Osoba $A$ nie chce siedzieć obok $B$, a osoba $C$ chce siedzieć obok $E$. Kto nie może siedzieć na środkowym miejscu?
Można zauważyć, że jeżeli osoba $D$ usiądzie na środku, to osoby $C$ i $E$ będą siedziały albo po jej lewej, albo po prawej, co wymusza (niezgodnie z warunkami zadania), żeby $A$ i $B$ siedzieli obok siebie. Tyle wystarcza, żeby na karcie konkursowej móc wpisać właściwą odpowiedź. Aby jednak takie rozumowanie było pełne, wypadałoby się przekować, że dla pozostałych osób na środku da się uzyskać chociaż jedno dobre rozmieszczenie. Organizatorzy nie wymagają jednak od uczniów tego zakończenia. I słusznie: nawet ambitni i sprytni trzecioklasiści nie muszą jeszcze rozumować na poziomie formalnym. Na wszystko przyjdzie czas.