
Pozycyjny system dziesiątkowy a przedszkolne dziecko
Jak wyjaśnić sześciolatkowi jak dodać do siebie 123 + 345?
Spis treści
Załóżmy, że mamy do czynienia z zdolnym sześciolatkiem, który interesuje się liczbami. Czy możliwe jest wytłumaczyć mu, jak dodawać do siebie liczby trzycyfrowe, nawet wtedy, gdy, jak mówią mądre głowy, należy przekroczyć próg dziesiątkowy? Moim zdaniem jest to możliwe, o ile dobrze się do tego przygotujemy.
System pozycyjny
Zanim coś wytłumaczymy dziecku, lepiej upewnijmy się najpierw, że sami dobrze to rozumiemy. Pamiętam ze szkoły jak na tablicy wykonywaliśmy przykładowo takie zapisy: $123 = 1 \cdot 100 + 2 \cdot 10 + 3 \cdot 1$. Z tego zapisu da się oczywiście wywnioskować, że jedynka jest cyfrą setek, dwójka jest cyfrą dziesiątek, zaś trójka oznacza liczbę jedności. Nie przypominam sobie, żebym wtedy rozumiał po co tak dziwnie rozpisywać coś co było krótkie i zrozumiałe (zapis $123$) w długie i skomplikowane działanie matematyczne, w dodatku zawierające sobie mnożenie, które jest daleko bardziej nietrywialne niż dodawanie.
Dodawanie liczb wielocyfrowych sprowadza się w zasadzie jedynie do zsumowania cyfr znajdujących się na tych samych pozycjach (jedności do jedności, dziesiątki do dziesiątek, setek do setek itd.). Oczywiście zachodzi przy tym ryzyko, że jedności uzbiera się na kolejną dziesiątkę, albo dziesiątek na kolejną setkę. Nie jest to może trywialne, ale przekazanie tego konceptu wydaje się być, co najmniej z teoretycznego punktu widzenia, możliwe.
Całe to rozważanie nie bierze pod uwagę, że nawet zdolne dzieci myślą o liczbach nieco inaczej: niekoniecznie ktokolwiek nauczył ich różnicy między liczbą a cyfrą (wielu dorosłych również nie czuje tej różnicy), a zrozumienie, że ta sama cyfra może oznaczać inną wartość zależnie od tego, na której pozycji stoi nie przychodzi łatwo.
Zauważmy, że już samo czytanie liczb dwucyfrowych jest niełatwe:
- liczby od $11$ do $19$ czytamy zaczynając od cyfry jedności i dodajemy naście,
- liczby od $20$ do $99$ czytamy zaczynając od cyfry dziesiątek, dodając do niej dziesiąt.
Sugerowałbym najpierw upewnić się, że dziecko rozumie różnicę między -dziesiąt, a -naście. Jeżeli dziecko jest zdolne, być może samo już zamanifestowało tę zdolność w zabawie w liczenie od $1$ do tysiąca przez pół dnia, aż głowa zacznie boleć wszystkich wokół, którzy tego słuchają.
Przy liczbach trzycyfrowych sytuacja jest jeszcze trudniejsza: czytając liczbę $314$ odczytujemy najpierw trójkę, potem czwórkę, a potem naście (jedynka na końcu). Jak ma się w tym połapać małe dziecko? Czy jest sens robić mu mętlik w głowie? Czy nie lepiej zaczekać, aż nadejdzie odpowiedni czas i będzie gotowe, żeby to wszystko “naturalnie” zrozumieć (cokolwiek miałoby to oznaczać)? Moim zdaniem, jeżeli dziecko samo pokazuje nam zainteresowanie liczbami, sygnalizując jakiś rodzaj fascynacji liczeniem to nie ma co czekać. Bez pomocy nauczyciela (lub rodzica), skończy się jedynie na tej fascynacji, a można ją przecież jakoś zagospodarować…
Fortel dydaktyczny: Liczby rzymskie
Na pierwszy rzut oka, system rzymski zapisu liczb może wydawać się jeszcze bardziej skomplikowany. Stare filmy z $1984$. roku mogą być podpisane MCMLXXXIV, co, w oczach niewprawnego, wygląda prawie jak szyfr.
Wyobraźmy sobie jednak, że do zapisu liczb dopuścimy jedynie znaki:
- I - oznaczające $1$,
- X - oznaczające $10$,
- C - oznaczające $100$.
Zapomnijmy o wszystkich trudnych i dziwnych regułach takich jak:
- mogą być co najwyżej trzy takie same znaki pod rząd,
- jeżeli symbol o większej wartości poprzedza symbol o mniejszej wartości to trzeba odjąć.
Niech liczba $17$ to po prostu XIIIIIII, a $147$ to CXXXXIIIIIII. Aby opowiedzieć o tym dzieciom, można po prostu pokazywać zapisy kolejnych liczb naturalnych, zaczynając od $1$, dorysowując systematycznie kolejne kreski na kartce lub tablicy. Gdy uzbiera się $10$, powinno być widać, że taki sposób zapisu jest nieefektywny i wprowadzenie symbolu X, żeby zastąpić dziesięć jedności jest czymś naturalnym. Dokładamy kolejne kreski do tego X i zachęcamy dziecko do czytania kolejnych wartości. W końcu uzbiera się XX, a niedługo później dziecko samo zrozumie regułę, o ile do tego czasu już to nie nastąpiło. Można potrenować i zamieniać liczby arabskie na “rzymskie” i na odwrót. Powinno być widać, że nie jest to trudne. W każdej grupie przedszkolnej, z którą pracowałem, znajdowałem co najmniej kilka dzieci, które złapały to w lot. Pozostali potrzebowali dodatkowych ćwiczeń lub nie byli jeszcze na poziomie chęci liczenia do tysiąca. Dla nich były przewidziane wcześniejsze zabawy w rozpoznawanie cyfr, przesuwanie klocków i upewnianie się, że jest ich dalej tyle samo, liczenie dziesiątkami etc.
Zanim jeszcze pokaże się symbol setki (C), można zapytać o “upraszczanie zapisu”:
- Jak możemy krócej zapisać liczbę XXXXIIIIIIIIIIII? Jak to zapisać z użyciem liczb arabskich?
- Która liczba jest większa: XXXXXXIII czy XXXXXIIIIIIIIIIIIIIIII? O ile większa?
- Ile symboli potrzeba, żeby zapisać liczbę $99$?
Nie każdy sześciolatek będzie w stanie od razu przy pierwszej prezentacji odpowiedzieć na takie pytania. Wymaga to operowania na zapisie symbolicznym, pewnej wyobraźni, ale jest to dopasowane do spodziewanego stadium rozwoju większości dzieci w grupie.
Przewaga systemu rzymskiego
W zaprezentowanym systemie ten sam symbol znaczy tyle samo, niezależnie od tego, na której pozycji stoi. Są tylko trzy różne symbole. Łatwo je zaprezentować na poniższym rysunku.
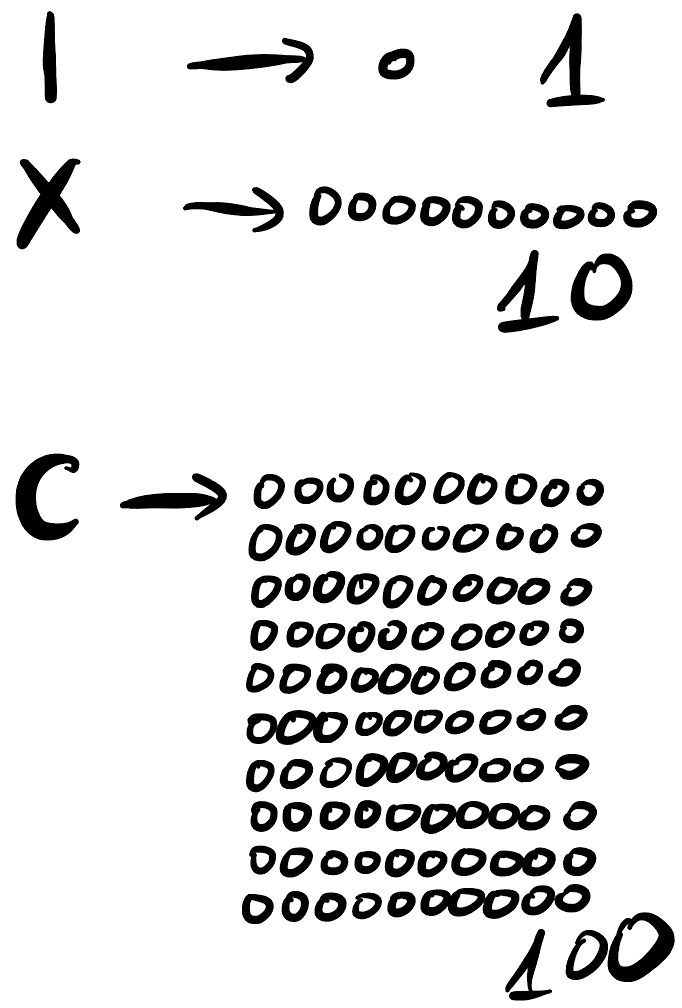
Znaczenie cyfr w uproszczonym systemie rzymskim.
Dodawanie liczb jest trywialne: wystarczy skleić ze sobą reprezentacje obu dodawanych liczb. Jeżeli wcześniej przygotowaliśmy sobie tekturowe kartoniki z narysowanymi kreskami, iksami i literami C, to mamy czym operować na dywanie. Wszelkie intuicje, które inaczej należałoby tłumaczyć dzieciom jako bliżej nieuzasadnioną regułę, że tak trzeba robić, wynikają wprost z zapisu i dziecko może do nich dojść samodzielnie. Dopasowujemy się przy tym do sposobu, w jaki uczy się dziecko: eksperymentując na pewnej liczbie przykładów samo dojdzie do zasad jakimi rządzą się liczby. Uczenie matematyki nie powinno polegać na wyjmowaniu z kapelusza zbioru zasad i krzyczeniu na niewinnych uczniów, że złamali którąś z nich. Jeżeli te zasady odkryją sami, będą je rozumieli, a błędy będą rzadkością.
Przykładowe zagadki dla dzieci
Weźmy przykładowe zadania:
- Jest XXXXXXIIII cukierków. Chcemy je podzielić między dwójkę dzieci. Ile dostanie każde z nich?
- Każde z pięciorga dzieci przyniosło po XII kredek. Ile kredek mają razem?
- Jaś miał XXXXXX złotych, ale kupił naklejki za XIIIIII złotych. Ile zostało mu pieniędzy?
Te zadania robi się (w uproszczonym systemie rzymskim) dokładnie tak samo, jak chcielibyśmy, żeby w przyszłości dziecko myślało o dzieleniu, mnożeniu i odejmowaniu. Jak na dłoni widać, że dodawanie $123 + 345$ jest tak samo łatwe jak dodawanie CXXIII + CCCXXXXIIIII, które daje wynik CCCCXXXXXXIIIIIIII.
Podsumowanie
Spuentuję mocno i (być może) dowcipnie: udało nam się osiągnąć efekt Rafaello. Koncept uproszczonych liczb rzymskich wyraża więcej niż tysiąc słów.
Jasnym jest, że jest to tylko wprawka do prawdziwego liczenia: system rzymski w tym wydaniu (i chyba w każdym) jest skrajnie nieefektywny, zarówno w zapisie jak i do dokonywania obliczeń. Całość służy do zbudowania prawidłowych intuicji, które należy wykorzystać już w typowych liczbach arabskich. Nie jestem pewien czy każde dziecko potrzebuje tej intuicji: zanim natrafiłem na zagraniczne źródła, w których przeczytałem o tej sztuczce dydaktycznej i przemyślałem sobie sposób jej prezentacji, udało mi się wcześniej dotrzeć do moich dzieci inaczej. Sprawdzając jednak tę metodę w trudniejszych warunkach, przy większych grupach przedszkolnych, które jako całość skupione są może przez kilka pierwszych minut zajęć, mogę powiedzieć, że jest to dobra droga na skróty.
Doradzam mimo wszystko być cierpliwym i zanim zacznie się eksperymentować, warto przemyśleć (na wzór tego co zrobiliśmy na początku tego posta) potencjalne trudności, które mogą wystąpić u dziecka z przyswojeniem materiału. Jeżeli nie zrozumiemy, gdzie może leżeć trudność, nie będziemy skuteczni. Dziecko najpierw musi być na odpowiednim stadium rozwoju, umieć odczytywać zapis symboliczny liczb, rozumieć różnice między -naście, a -dziesiąt i wtedy jest sens próbować. Jeżeli dobrze się do tego przygotujemy (na przykład przygotowując sobie odpowiednie materiały do manipulacji przez dziecko) to będzie ciekawie: dla dziecka i dla rodzica. Tego oczywiście życzę wszystkim zainteresowanym, zachęcam przy tym do dyskusji w komentarzach i podzielenia się swoimi doświadczeniami i pomysłami na naukę matematyki wśród najmłodszych.