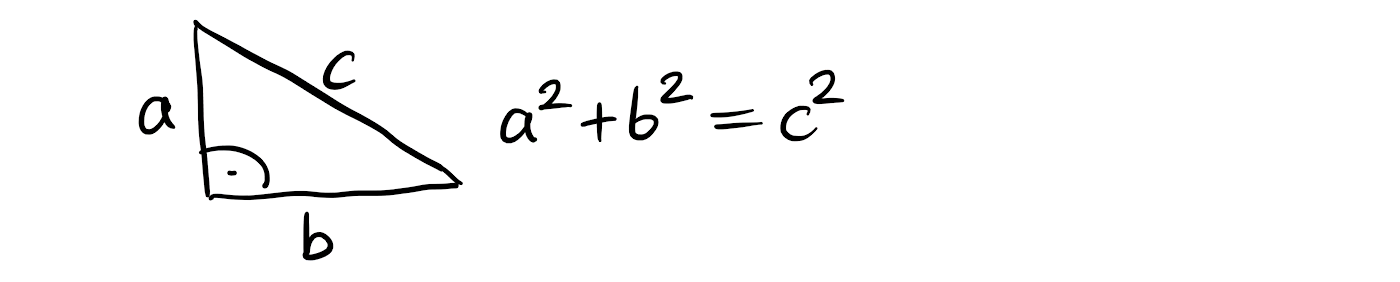
A ma Pan dowód? Nie ma dowodu, że Pitagoras wiedział o...
Jak uczyć, żeby nie nauczyć na przykładzie twierdzenia Pitagorasa?
Spis treści
Jako człowiek zainteresowany nauczaniem, jestem zapisany na kilka newsletterów edukacyjnych. W szczególności, co tydzień przychodzi do mnie e-mail ze strony 45minut.pl. Nauczyciele mogą tam wymieniać się różnymi materiałami - sprawdzianami, testami, konspektami czy planami rozwoju zawodowego. Jakiś czas temu na cotygodniowej liście publikacji znalazłem Scenariusz lekcji matematyki w klasie 7 z podtytułem Uczniowie podczas lekcji zapoznają się z Twierdzeniem Pitagorasa i potrafią zastosować je w zadaniach. Wygląda mi na to, że komuś się chciało i zupełnie za darmo opublikował dla wszystkich materiał jak to powinno się robić. Brzmiało to dla mnie dostatecznie interesująco, żeby przejrzeć publikację. Niestety, wnioski z lektury dokumentu nie napawają optymizmem. Już wtedy wiedziałem, że będę miał o czym pisać na blogu, gdy go w końcu założę.
Materiał przygotowany przez typowego nauczyciela
Materiał, o którym mowa, można znaleźć tutaj. Cele brzmią dumnie: uczeń ma poznać treść twierdzenia Pitagorasa, nauczyć się je zastosować, a nawet ma się kształtować jego logiczne myślenie. Do realizacji tych celów, według autorki materiału, pomocne będzie:
- zapoznanie uczniów z treścią twierdzenia Pitagorasa (i poinformowanie uczniów, że twierdzenie dotyczy jedynie trójkątów prostokątnych),
- rozwiązanie zadania o obliczeniu długości przeciwprostokątnej trójkąta prostokątnego o przyprostokątnych 8 cm i 6 cm,
- praca w parach z wyciętymi szablonami z trójkątami (uczniowie mają najpierw obliczyć długości przeciwprostokątnych, a potem sprawdzić swoje obliczenia mierząc boki szablonu),
- rozwiązanie zadania odwrotnego (dana jest długość jednej z przyprostokątnych oraz długość przeciwprostokątnej, obliczyć długość drugiej przyprostokątnej),
- ponowna praca w parach z szablonami (uczniowie mają obliczać teraz długości jednej z przyprostokątnej jak w zadaniu powyżej).
Prawda, że ciekawie? Zamiast klepać formułki W trójkącie prostokątnym suma kwadratów długości przyprostokątnych jest równa kwadratowi…, uczniowie będą rozwiązywać zadania przy tablicy oraz w parach, wykonywać doświadczenia, sprawdzać praktycznie wiedzę teoretyczną wykonując pomiary. Tak wiele w ciągu jednych, 45-minutowych zajęć.
Widzę tutaj tylko jeden (bardzo duży) problem. Konspekt dotyczy pierwszych zajęć w tym temacie. Nauczyciel prezentuje uczniom nieoczywiste twierdzenie matematyczne. Bez dowodu. Gdyby to było w pierwszych klasach szkoły podstawowej to uczniowie może zadaliby nauczycielowi naturalnie narzucające się pytanie Dlaczego tak jest?, ale to jest przecież konspekt zajęć w klasie siódmej. Naturalna ciekawość ucznia i wiecznie powtarzające się pytanie A czemu? zostały już dawno stłumione przez wcześniejsze lata edukacji.
Nie mogę pojąć, że ktoś, komu przecież się chciało (przygotować ten materiał i podzielić z innymi nauczycielami) jest gotów przepuścić taką okazję do pokazania uczniom czegoś ciekawego. Uczniowie w klasie siódmej szkoły podstawowej mają około 12-13 lat i według wszelkich teorii o nauczaniu powinni być w stanie już rozumować na poziomie formalnym. Dotychczas rozwiązywali już równania matematyczne, poznali sposoby dodawania ułamków, wzory na obliczanie pól wielu figur geometrycznych, cechy przystawania trójkątów czy reguły podzielności. Czy nie są gotowi, żeby zrozumieć dowód matematyczny? Czy nie są gotowi, żeby powiedzieć im prawdę, że twierdzenie staje się twierdzeniem dopiero wtedy, gdy upewnimy się, że jest prawdziwe i że dopiero od tego momentu można je stosować?
Scenariusze innych lekcji z internetu
Wpisałem w wyszukiwarkę Google zapytanie twierdzenie Pitagorasa scenariusz lekcji. Na pierwszej stronie wyników wyszukiwania znalazłem jeszcze inne “ciekawe” pomysły na przeprowadzenie zajęć. Między innymi:
- rozwiązywanie rebusu, żeby odkryć temat lekcji, a następnie układanie treści twierdzenia Pitagorasa z rozsypanych wyrazów (tak, nie żartuję) - a jednym z celów szczegółowych zajęć jest, uwaga, potęgowanie pierwiastków!,
- oglądanie prezentacji multimedialnej o postaci Pitagorasa z Samos, samodzielne odkrywanie dowodu twierdzenia przez uczniów, posługując się układankami matematycznymi (niestety, nie wyolbrzymiam).
Oczywiście, żeby być przy mojej ocenie uczciwym, znalazłem też kilka innych materiałów, w których autorzy zauważają konieczność pokazania uczniom dowodu poprawności.
Problem niestety nie dotyczy jedynie twierdzenia Pitagorasa. Szanowny Czytelniku, czy pamiętasz jak sprawdzić czy liczba $34\ 128$ jest podzielna przez $3$ bez reszty? Obstawiam, że możesz sobie przypomnieć, że należy sprawdzić czy suma cyfr ($3 + 4 + 1 + 2 + 8 = 18$) jest podzielna przez $3$. A czy pamiętasz, żeby nauczyciel w szkole podstawowej powiedział Ci dlaczego to działa?
Ze szkoły podstawowej pamiętam również, wprowadzony zupełnie bez celu, sposób na obliczanie największego wspólnego dzielnika i najmniejszej wspólnej wielokrotności dwóch liczb za pomocą rozkładu na czynniki pierwsze. Temat ten nie powtórzył się przez kolejne dwa-trzy lata. Jasne, że dodawaliśmy w tym czasie ułamki, a więc musieliśmy sprowadzać je do wspólnego mianownika, ale czy robiło się to właśnie tymi metodami? O algorytmie Euklidesa nie było nawet wzmianki. Może to i nawet dobrze: boję się, że niektórzy nauczyciele mogliby skupić się na postaci Euklidesa lub układaniu napisu NWD z literek N, W oraz D zamiast uzasadnieniu własności $\operatorname{NWD}(a, b) = \operatorname{NWD}(b, a \bmod b)$ i wniosków jakie z niej płyną.
Niestety, wiem, że w szkole w tym zakresie nic się nie zmieniło od czasu kiedy sam byłem uczniem. Nawet uczniowie klas pierwszych z dobrych liceów, których zdarza mi się uczyć, potrzebują chwili na przyzwyczajenie się do nowego trybu zajęć, gdy analizujemy poprawność każdego kroku, a dowody pojawiają się ciągle, bo wiele narzucających się, oczywistych algorytmów okazuje się być niepoprawnych i zwyczajnie potrzebujemy narzędzi, żeby upewniać się, czy to co robimy ma sens. Długo zajmuje mi przekonanie uczniów, że Dlaczego to miałoby nie działać? jest złym pytaniem i że od dawna powinni zadawać sobie pytanie Dlaczego to działa?. Niektórych udaje się przekonać, ale nie wszystkich. Zastanawiam się, co dzieje się w innych szkołach średnich, gdzie nauczyciele mogą nie mieć motywacji lub zasobów, aby skorygować błędne zrozumienie matematyki przez swoich uczniów. Czy tam też popełniane są podobne błędy jak w edukacji na poziomie szkoły podstawowej? Teoretycznie nie powinno tak być, bo dowody, w ograniczonej formie i ilości, pojawiają się na maturze z matematyki. Ale jak jest naprawdę? Jeszcze tego nie sprawdziłem.
Konkretny przykład dlaczego warto dowodzić
Rozważmy dla odmiany problem algorytmiczny: wydawanie reszty. Wrzucamy 5 zł do automatu, kupujemy batonik za 3,50 zł. Automat wydaje 1,50 zł reszty. Piętnaście dziesięciogroszówek. Ma to sens? Oczywiście, że nie: automat wydałby raczej złotówkę i pięćdziesięciogroszówkę. A jak to wyznaczyć w ogólnym przypadku? Nikt z nas nie był tego uczony w szkole, ale w zasadzie każdemu narzuca się następujący pomysł: wydawaj systematycznie jak największy nominał jaki możesz i zmniejszaj w ten sposób pozostałą kwotę do wydania. Sęk w tym, że to nie działa. Niech dostępne nominały to $1$, $99$ oraz $101$. Niech kwota do wydania to $198$. Algorytm wyda $101 + 1 + 1 + 1 + \ldots + 1$, a mógłby $99 + 99$. Właśnie dlatego Dlaczego to miałoby nie działać? nie jest właściwym sposobem myślenia o algorytmach czy twierdzeniach matematycznych. Na matematyce moglibyśmy przynajmniej tego się nauczyć.
Twierdzenie Pitagorasa a podręczniki szkolne
Skoro nauczyciele opracowują własne scenariusze lekcji, w których popełniają (moim zdaniem) kardynalne błędy, to może robią to dlatego, że nie mają odpowiednich narzędzi do pracy? Sprawdziłem jak wygląda materiał o twierdzeniu Pitagorasa w podręcznikach szkolnych. Podręcznik z wydawnictwa GWO dostępny jest online tutaj. Wydawnictwo, publikując treść podręcznika w internecie, najwyraźniej nie ma się czego wstydzić: w podręczniku rzeczywiście przedstawiony jest jeden ze sposobów uzasadnienia twierdzenia. Nie powiedziałbym, że najprostszy, ale co najmniej temat nie został pominięty. Nawet nauczyciele, którzy uważają, że przedstawienie postaci Pitagorasa jest w tym miejscu kluczowe, powinni być zadowoleni: w podręczniku również znajduje się odpowiednia wzmianka.
Podobnie chyba jest w podręczniku Nowej Ery. Już w spisie treści znajduje się dział Twierdzenie matematyczne i jego dowód, więc zaczynam być spokojny. Do podręcznika z WSiP nie udało mi się dotrzeć. Wygląda jednak na to, że problem nie tkwi w podręcznikach.
Konsekwencje nauczania bez dowodów
Z mojego doświadczenia wynika, że uczniowie często nie mają pojęcia, jak udowodnić twierdzenia czy własności, które stosują do rozwiązywania zadań. Co gorsza, zdają się nie odczuwać potrzeby zrozumienia tych podstaw, ani ze strony nauczyciela, ani z własnej inicjatywy. Matematyka, która rzekomo miała być królową nauk, a przez którą prowadzi moim zdaniem najprostsza (pewnie nie jedyna) droga do osiągnięcia zdolności logicznego myślenia, często nauczana jest jako zestaw reguł do zapamiętania, a nie jako pole do zrozumienia i eksploracji. Nic dziwnego, że taka matematyka się wielu uczniom (zdolnym lub nie) nie podoba. Powiedziałbym, że wcale tak wiele nie brakowało, żebym również matematyki nie lubił. Polubiłem ją na poważnie dopiero wtedy, gdy przyszło mi mierzyć się z zadaniami olimpijskimi.
To jak to zrobić dobrze?
A może dowód twierdzenia Pitagorasa jest trudny i nauczyciele słusznie go omijają? Absolutnie nie. Najprostszy wygląda chyba tak: weźmy cztery przystające trójkąty (prostokątne) i ułóżmy je jak na obrazku poniżej:
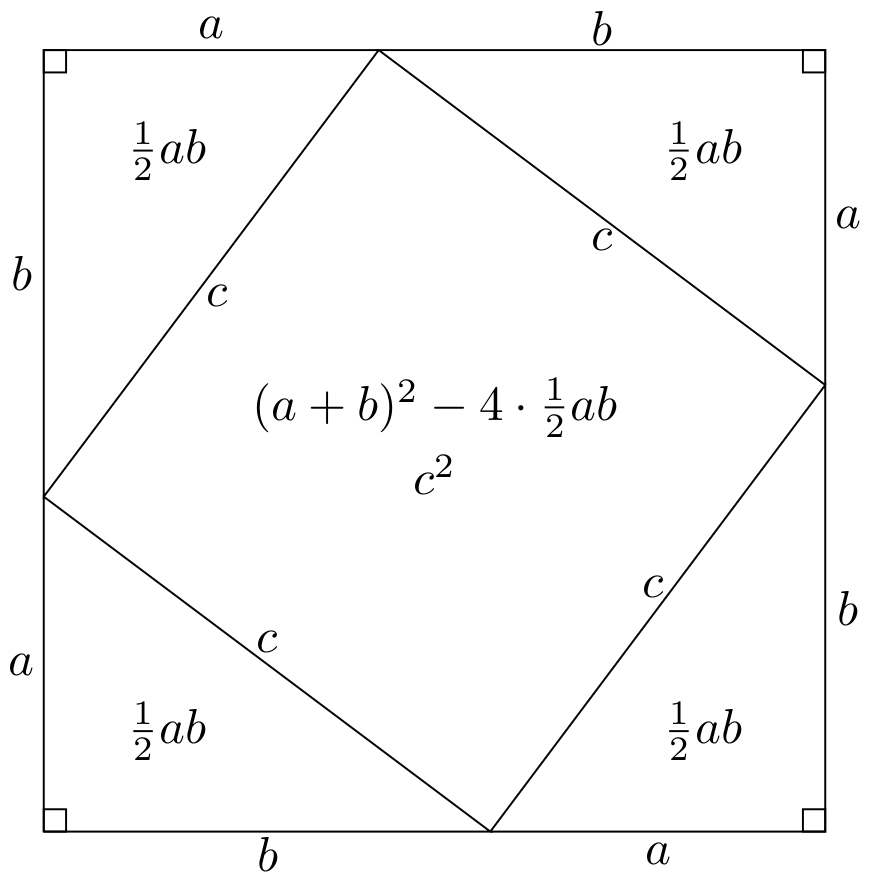
Dowód twierdzenia Pitagorasa.
Policzmy pole powstałej figury w środku trójkątów. Po pierwsze zauważamy, że jest ona kwadratem (każdy kąt jest prosty, co wynika z sumy $90^{\circ}$ miar dwóch kątów wewnętrznych poza kątem prostym w każdym z trójkątów prostokątnych, a boki są równej długości, bo trójkąty są identyczne). Pole więc wynosi $c^2$. Z drugiej strony to samo pole można obliczyć licząc pole dużego kwadratu i odejmując cztery pola trójkątów (nawet nie trzeba znać wzoru na pole trójkąta, bo każdy z trójkątów jest połówką prostokąta): $(a+b)^2 - 4 \cdot \frac{ab}{2} = (a+b)^2 - 2ab = a^2 + b^2$. Pole tej samej figury jest takie samo, niezależnie od tego jak je policzymy, a więc $c^2 = a^2 + b^2$ i koniec dowodu.
Ktoś mógłby się już obruszyć i powiedzieć ale musieliśmy użyć wzorów skróconego mnożenia przy przejściu $(a+b)^2$. Nie musieliśmy, mogliśmy po prostu naiwnie zapisać $(a+b)^2 = (a+b)(a+b)$ i wymnożyć, żeby ów wzór wyprowadzić. A najlepiej byłoby po prostu założyć, że w klasie siódmej, gdy podstawowe wyrażenia algebraiczne mamy już za sobą, poniższy mem się tym razem nie sprawdził.

Mem z Bogusławem Lindą o wzorach skróconego mnożenia.
Tak, za każdym razem, gdy wzory skróconego mnożenia się jednak przydają, wspominam uczniom (studentom też), że właśnie upływa nam dzień z potrzebą użycia wzorów skróconego mnożenia. Dowcip raz na kilkanaście minut zajęć i tak jest potrzebny, żeby zresetować uwagę uczniów, więc taki jak powyższy chyba bardzo nie zaszkodzi.
Może dobrym zadaniem domowym po pierwszych zajęciach o twierdzeniu Pitagorasa byłoby znajdź w internecie inny dowód poprawności twierdzenia niż ten, który poznaliśmy na zajęciach? A nie, wróć, zadania domowe są teraz passé.
Podsumowanie
Uważam, że nauczyciele matematyki powinni zawsze prezentować uczniom dowód poprawności twierdzenia lub nieoczywistej własności. Bez tego uczniom brakuje zrozumienia zasady, której używają. Po prostu: nie widzę usprawiedliwienia dla nauczycieli matematyki, którzy tego nie robią. Jeżeli nie potrafią, zamiast szukać ewentualnej riposty dla ucznia, który o dowód zapyta, powinni poświęcić chwilę, żeby się doedukować, na przykład wpisując w wyszukiwarce frazę Pythagorean theorem simplest proof. Zajmie mniej czasu, nauczyciel się czegoś nauczy, a i lekcja będzie bardziej pouczająca. Szkoda, że mało który nauczyciel matematyki to przeczyta.
Czytelniku, a czy Ty pamiętasz, jak w Twojej szkole przedstawiane było twierdzenie Pitagorasa lub ogólniej, inne twierdzenia/własności? Przykładowo: cecha podzielności przez $3$, wzór na pole trapezu, objętość ostrosłupa lub stożka albo prawa działań na potęgach czy wzory skróconego mnożenia. A może jednak przesadzam i nauczyciele pokazują uczniom więcej niż mi się wydaje? Zostaw swój komentarz poniżej.